지금까지 논문 스터디 학회 활동과 개인적으로 정리했던 논문들을 하나씩 올려보려고합니다.
과거에 정리한 글을 올리면서 잊어버렸던 내용을 상기시키면서 조금씩 부족한 부분을 최대한 수정해 글을 올리겠습니다.
과거에 정리했던 논문인지라 부족한점이 많을 수 있어 부족한 부분은 알려주시면 감사하겠습니다.
0. Abstract
● 2가지 모델을 훈련시켜 적대적인 프로세스(경쟁)을 통해 generative model을 평가하는 새로운 프레임워크를 제안
여기서 말하는 2가지 모델은 Generative model(G)와 Discriminative model(D)이다. Traning data의 분포를 모사해 데이터를 제공하는 G와 해당 데이터가 G가 만든것인지, 원본인지 판별하는 D이다.
G는 D가 실수할 확률을 높이는 방향으로 학습된다. 즉, D가 잘 구별하지 못하도록 이미지를 생성한다.
이 프레임워크는 minimax 게임과 비슷하다. 임의의 경우에서 G 와 D는 각각 유일한 솔루션이 존재하며 모두 1/2의 확률을 갖는다. G와 D가 다층퍼셉트론의 구조를 가지고 있다고 정의한 경우 역전파를 이용한 학습이 가능하다. 이는 데이터를 훈련하거나 생성할때 다른 어떤 네트워크나 마르코프 체인이 필요가 없다.
이 실험은 생성된 샘플에 대해 질적 및 정량적 평가를 통해 프레임웤크의 가능성을 보여준다.
1. Introduction
딥러닝은 계층적이고 풍부한 모델을 학습하여 이미지, 음성을 포함한 오디오 파형, 자연어 특징과 같은 데이터를 인공지능을 활용하여 확률로 나타내어 준다. 여태까지 가장 성공한 딥러닝은 모두 고차원의 특성, 많은 입력을 가지는 구별하는 모델을 포함했다. 이런 성공들은 역전파와 드롭아웃 알고리즘에 기초하였으며, 선형적인 단위를 사용하여 가중치에 잘 작용하여 높은 성능을 낼 수 있었다. 하지만 Deep generative model은 제어하기 힘든 수많은 Maximum Likelihood Estimation(MLE, 최대우도추정)과 같은 전략들에서 나오는 많은 확률론적 계산의 어려움과 생성모델 에서 부분적 선형유닛의 이점을 활용하는 것의 어려움으로 인해 좋은 성능을 내지는 못했다.
우리는 이러한 어려움을 피하는 새로운 생성모델을 소개한다.(adversarial nets)
G: Generative model
- GAN은 생성모델로 이미지, 음성, sequentail data등 원하는 형태의 데이터를 만드는 모델이다.
- Discriminative model을 상대로 완벽하게 속이고자 한다. -> training data의 분포를 모사함
D: Discriminative model
- 실제 데이터와 생성 모델이 만들어낸 데이터를 구별
- sample 데이터가 G로부터 나온 데이터가 아닌 실제 training data로부터 나온 데이터일 확률을 추정

2. Realtion work
PASS
3. Adversarial nets
Adversarial modeling framework는 모델이 모두 mulitlayer perceptron일때 가장 적용하기 쉽다.
입력데이터 x에 대해 생성된 (p_g)를 학습하기 위해 입력에서 더해질 noise 변수를 p_z(Z)라 정의하고 데이터 공간에 대한 매핑을 G(z; θg)로 표현하는데, 여기서 G는 매개 변수를 가진 다층 퍼셉트론에 의해 표현되는 미분 가능한 함수이다.
또한 단일 스칼라를 출력하는 두 번째 다층 퍼셉트론을 D(x; θ_d)라고 정의한다. D(x)는 x가 p_g가 아닌 진짜 데이터 분포일 확률을 단일 스칼라로 나타낸다. 여기까지 p_g를 출력하는 G(generative model)과 p_g가 아닌 실제 데이터를 구분하는 D(discriminative model)를 정의하는 과정이다.
다음은 D가 훈련 샘플과 G의 샘플 모두 올바르게 구별하도록 훈련시킨다. 동시에 log(1 − D(G(z)))를 최소화하도록 G를 훈련시킨다. 학습 초반에는 G가 생성해내는 이미지는 D가 G가 생성해낸 가짜 샘플인지 실제 데이터의 샘플인지 바로 구별할 수 있을 만큼 형편없어, D(G(z))의 결과가 0에 가깝다. 즉, z로 부터 G가 생성해낸 이미지가 D가 판별하였을 때 바로 가짜라고 판별할 수 있다고 하는 것을 수식으로 표현한 것이다. 그리고 학습이 진행될수록, G는 training data 분포를 모사하면서 D(G(z))의 값이 1이 되도록 학습한다. 이는 G가 생성해낸 이미지가 D가 판별하였을 때 진짜라고 판별해버리는 것을 표현한 것이다.
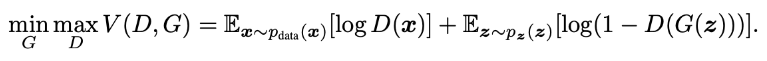
첫번째 항: real data x를 discriminator 에 넣었을 때 나오는 결과를 log취했을 때 얻는 기댓값
두번째 항: fake data z를 generator에 넣었을 때 나오는 결과를 discriminator에 넣었을 때 그 결과를 log(1-결과)했을 때 얻는 기댓값

- 검은 점선이 data generating distribution (실제 데이터 분포)
- 파란 점선이 discriminator distribution (분류 분포)
학습을 반복하다보면 가장 구분하기 어려운 구별 확률인 0.5 상태가 된다. - 녹색 선이 generative distribution (가짜 데이터 분포)
학습과정
- Noise로부터 G를 통해 가짜 데이터를 만들고 이를 D에 Input으로 넣습니다. (Feed Forward)
- 일반적인 Neural Network는 Input과 Hidden Layer를 거쳐 Output을 계산하는 것까지를 Feed Forward라 하는데, G는 G의 아웃풋을 다시 D의 Input으로 넣어 Output까지 계산한다. G의 목적이 D를 속이는 것이고 D의 에러를 통해 G의 Back Propagation을 계산하기 때문에 G의 Feed Forward는 D까지 거치게 되는 것이다.
- G의 입장에서 상기시켜보면 G의 목적은 D를 속이기 위해서입니다. G는 D를 속이는 방향으로 G의 Weight를 업데이트 해야한다. 즉, D의 입장에서 G가 만들어낸 가짜 데이터를 진짜로 판단하도록 G의 웨이트를 업데이트 하는 것 이다.
이 과정을 위해 D의 에러에서부터 G까지 weight를 역전파 시킨다. 이때 D의 웨이트는 업데이트하지 않는다. D는 단지 G의 웨이트를 구하기 위해 에러를 전파시키기만 할 뿐, 웨이트는 업데이트 하지 않습니다 . 이 과정을 Weight Freezing이라 합니다. 이 과정을 무한히 반복하면 진짜 데이터와 가짜 데이터를 구분할 확률이 0.5에 수렴한다(Figure1.(d)).
생성자 모델은 판별자 모델을 속이기 위해 최대한 진짜 같은 데이터를 만들고, 판별자는 반대로 위조 데이터와 진짜 데이터를 감별하려고 실력을 키워나간다. 이후 판별자의 예측 결과에 따라 각 모델의 Loss가 결정되고, 서로 학습을 반복하게 된다. 이런 경쟁구도 속에서 두 모델의 능력이 상호 발전되어가고, 결론적으로는 판별자 모델이 생성자 모델이 만드는 데이터를 구별하기 힘들 정도로 만들어 나가는 것이 목적이다.
4. Theoretical Results
G는 확률 분포 p_g를 z ~ p_z일 때 얻은 표본 G(z)의 분포로 암묵적으로 정의한다. 따라서, 우리는 충분한 양과 훈련 시간이 주어진다면 Algorithm 1이 p_data의 좋은 추정치로 수렴되기를 바란다. 이 섹션의 결과는 non-parametric하게 수행된다. 예를 들어 확률 밀도 함수의 공간에서의 수렴하는걸 학습함으로 써 무한 용량을 가진 모델을 표현하겠다고 말했다.
섹션 4.1에서 이 minmax game이 p_g=p_data에 대한 global optimum임을 보여줄 것이다.
섹션 4.2에서 Algorithm 1이 value function V(G,D)를 최적화하여 원하는 결과를 얻는다는 것을 보여줄 것이다.
Algorithm 1
적대신경망의 훈련을 위한 미니배치 확률적 경사 하강법, 하이퍼파라미터 k는 구별모델에 적용하기 위한 스텝을 나타낸다. 우리는 실험에서 k =1 을 사용하였다.

1. noise prior p_g(z) 로부터 noise 시킨 m개의 미니배치 {z(1),...,z(m)} 샘플을 만든다.
2. 데이터 생성분포 p_data(x) 로부터 미니배치 m개의 샘플 {x(1),...,x(m)}을 평가한다.
3. 확률적 경사 상승법을 이용하여 D를 업데이트한다.
k번의 스텝이후
k-1. noise prior p_g(z) 로부터 noise 시킨 m개의 미니배치 {z(1),...,z(m)} 샘플을 만든다.
k-2. 확률적 경사 하강법을 이용하여 G를 업데이트한다.
이 실험은 momentum을 이용한 옵티마이저를 사용했다.
4.1 Global Optimality of p_g = p_data
우선 주어진 G에 대해 최적의 D가 있다고 가정한다.
Proposition 1 : G가 고정되어 있을 때 최적의 D는 다음과 같다.

Proof 1 : 주어진 어떤 G에 대해 D의 훈련법은 V(G,D)의 값을 최대화 시키는 것이다.

이 식이 최대값을 갖기 위해 만족해야할 조건을 찾아보도록 하겠다.
(0,0)이 아닌 (a, b) ∈ R^2가 있을 때 y → alog(y) + blog(1 − y)가 최대값을 가지려면 어떻게 하면 되는지 알게되면 V(G, D)가 최대값을 가질 조건을 알 수 있다. 미분한 값이 0이 되는 시점의 y를 알면 된다.
미분을 하면 a/y - b/(1-y)가 되고 a/y - b/(1-y) = 0이라는 식을 세우고 y에 대해 정리를 하면 y = a/(a + b)가 된다.
이를 V(G, D)의 값을 보며 a, b를 바꿔보면 a = p_data(x), b = p_g(x)가 된다.
그럼 앞선 Proposition에서 세운 최적의 D가 나오게 되고 최적의 D는 올바른 식이라는 것을 알 수 있다.

p_data, p_g는 0~1 사이에 있는 값입니다. 0~1이 아닌 경우는 고려하지 않기에 논문에서값의 범위를 [0, 1]로 정했다.
(Proof 1)
D를 학습시키는 목적은 조건부 확률 P(Y=y|x)의 log-확률(log-likelihood)을 최대화하기 위함으로 해석될 수 있다. 여기서 Y는 입력 데이터 x가 진짜 데이터(p_data)에서 온건지(y=1) 아니면 모방해서 만든 데이터(p_g)에서 온건지(y = 0) 나타낸다. 그러므로 앞선 minmax게임을 다음과 같은 global minimum of the virtual training criterion C(G)로 재구성 할 수 있다.

Theorem 1. 가상 훈련 기준 C(G)의 전역 최소값은 p_g = p_data인 경우에만 달성된다. 이 시점에서 C(G)는 -log(4)라는 global minimum 값을 달성합니다.
(식1에 따르면) p_g=p_data에 대해 D_G(x) =0.5이다. 그렇다면

가 되는 것을 확인할 수 있다. log(0.5)의 기대값은 log(0.5)로 같기 때문에 -log(4)가 된다. 위의 식이 p_g=p_data에 대해 최적의 C(G)값인지는 다음 식을 확인하라.

그리고 이 식을 C(G) = V(D_G, G)에서 빼면 다음과 같은 값을 얻을 수 있다.

KL은 Kullback-Leibler 발산이다. 우리는 이전 표현에서 모델의 분포와 데이터 생성과정에서 Jensen-Shannon발산을 발견했다.

두 분포 사이의 Jensen-Shannon 발산은 항상 음이 아니고 그것들이 같을 때만 0이기 때문에, 우리는 C∗ = -log(4)가 C(G)의 global munimum이며, -log(4)를 얻을 수 있는 유일한 조건은 p_g=p_data이라는 걸 증명 했다.
즉, 생성모델이 완벽하게 실제 training data 분포를 완벽히 복제해야 virtual training criterion C(G)의 global minimum을 얻을 수 있는 것이고 이는 생성모델이 데이터를 완벽하게 생성했다고 볼 수 있다.
4.2 Convergence of Algorithm 1
이 알고리즘이 잘 풀어보는지 증명 해보도록 한다.
Proposition 2 : G와 D가 충분한 능력을 가지고 있고 Algorithm 1의 각 단계에서 D는 최적의 G에 도달할 수 있으며 p_g는 criterion을 향상 시키는 방향으로 업데이트 되어 p_data로 수렴한다.
위에서 쓰인 기준과 같이 V(G, D) = U(p_g, D)를 p_g의 함수로 간주한다.
우리는 U(pg, D)는 p_g에 있는 볼록한 부분(convex)이라는 걸 눈여겨 봐야한다.
볼록 함수의 상한을 하위미분한 것은 최대값을 얻을 수 있는 점에서 함수를 미분한게 포함되어 있는데, 수학적으로는 'f(x) = supα∈A fα(x) 와 fα(x)가 모든 α에 대해 x에서 convex일 때, β = argsupα∈A f_α(x)인 조건 아래 ∂fβ(x) ∈ ∂f 이다'로 표현할 수 있다. 이를 좀더 알기 쉽게 나타내면 "corresponding한 G가 있을 때 최적의 D에서의 p_g를 만드는데 사용될 gradient를 계산하는게 U(p_g, D)에 들어있다"고 보면 된다고 한다.
supD U(pg,D)는 C(G)를 증명할 때 증명되었듯 균일한 global optima를 가진 p_g에 있는 convex이므로 p_g를 조금씩, 그러나 충분할 정도로 업데이트 하다보면 p_g는 p_x에 수렴하게 된다.
이는 해당 G가 주어진 최적 D에서 p_g에 대한 경사 하강법을 계산하는 것과 같다.
이론적으로는 이렇게 완벽한 D, G를 만들 수 있지만 실제로 만들려고 할 때는 그렇지 않습니다.
adversarial nets은 G(z; θ_g)를 통해 제한된 값의 집합인 p_g 분포를 나타내게 되므로, p_g 자체보다는 G의 parameter인 θ_g를 최적화 했다고 한다. p_g를 수렴시킨다는 걸로 증명한게 적용되지 않았다 볼 수 있다. 그러나, 최적화된 θ_g를 가진 G는 실전에서 뛰어난 성능을 자랑한다. GAN이 이론적으로 보장이 없음에도 불구하고 사용할 수 있는 합리적인 모델임을 을 보여준다.
5. Experiments
- MNIST, Toronto Face Database(TFD), CIFAR-10에 대해 학습 진행
- G는 rectifier linear, sigmoid 활성화 함수를 혼합하여 사용, D는 maxout activation 사용
- D를 학습시킬 때 Dropout사용
- 이론적인 프레임워크에서는 generator의 중간층에 dropout과 noise를 사용할 수 있지만, 실험에서는 노이즈를 generator net 맨 아래 계층에 input으로만 사용함.
- 이 실험에서는 G로 생성된 sample에 Gaussian Parzen window맞추고, 해당 분포에 따른 log-likelihood를 알려줌으로써 P_g에 따른 test set data 확률을 추정

아래의 그림에는 교육 후 G에서 추출한 샘플이 나와 있다. 이 샘플이 기존 방법에 의해 생성된 샘플보다 낫다고 주장하지 않지만, 우리는 이러한 샘플이 적어도 문헌의 더 나은 생성 모델과 경쟁하고 있으며 적대 신경망의 가능성을 강조한다.

6. Advantages and disadvantages
새로운 프레임워크는 이전과 비교하여 장단점이 존재한다.
단점은 일차적으로 p_g(x)의 명시적 표현이 없고 훈련 중에 D를 G와 잘 동기화해야 한다는 것이다. 여기서 동기화를 잘해야 한다는 것은 G가 D의 학습 없이 너무 많이 학습 되어선 안된다는 뜻이다. G만 계속해서 가중치를 조정할 경우 G는 p_data의 분포를 따르는 데 충분한 다양성을 지닐수 없게되는 Helvetica scenario에 빠지게 되므로 G만 학습해선 안된다.
장점은 마르코프 체인이 필요하지 않고 기울기 조정을 위해 역전파만 사용되며, 학습중 inference가 필요하지 않으며, 다양한 기능이 모델에 통합될 수 있다는 것이다. adversarial nets framework와 다양한 함수를 합칠 수 있다는 것을 장점으로 말했다. 다음의 표를 통해 Adversarial models과 다른 것들을 비교할 수 있다.

앞서 말한 장점들은 주로 계산적인 측면에서 말한것이다. 또한 adversarial nets framework는 statistical advantage도 가지고 있다. 모델을 만들 때, 데이터 예제를 통해 직접 가중치를 업데이트하는게 아니라 D의 기울기 조정만으로 가중치를 업데이트 할 수 있다. 즉 입력 데이터의 구성요소들이 generator의 가중치 속에 직접적으로 복사되는게 아니라는 뜻과 같습니다. 그리고 매우 날카롭고 퇴화된 분포를 나타낼 수 있다는 것도 장점으로 꼽았습니다. 반면 Markov chain에 기초한 방법은 다양한 모드와 혼합될 수 있도록 분포가 다소 흐릿할 것을 요구한다.
1) 단점
- pg(x)가 명시적으로 존재하지 않음.
- D와 G가 균형을 잘 맞춰 동기화 되어야함(Helvetica scenario)
2) 장점
- 학습중 어떠한 inference가 필요 없다.
- 다양한 함수들이 적대적신경망 프레임워크에 접목될 수 있음
- 마크코브 체인을 쓸 때 보다 더 선명한 이미지를 얻을 수 있음
- 마크코브 체인이 전혀 필요가 없고 가중치를 얻기 위해 역전파 만이 사용됨.
7. Conclusions and future work
이 프레임워크는 많은 간단한 확장을 허용합니다.
-
G,D 양쪽에 입력으로서 c를 더하면 conditional generative model로 발전시킬 수 있음 (CGAN) = p(x|c)
-
Learned approximate inference는 주어진 x를 예측하기 위해 보조 네트워크를 훈련함으로써 수행될 수 있다. 이것은 wake-sleep 알고리즘으로 학습된 inference net과 유사하지만 G가 학습을 마친 후 고정된 G에 대해 inference net이 훈련될 수 있다는 장점이 있다.
-
parameters를 공유하는 conditionals model를 학습함으로써 다른 conditionals models을 근사적으로 모델링할 수 있다. 특히 MP-DBM의 stochastic extension을 구현하기 위해 적대신경망을 사용할 수 있다.
-
Semi-supervised learning : 제한된 레이블이 있는 데이터 사용할 수 있을 때, classifiers의 성능 향상시킬 수 있다.
- 효율성 개선: 학습 중에 G,D를 조정하는 더 나은 방법을 찾거나 학습하는 동안 sample z에 대한 더 나은 분포를 결정함으로써 학습의 속도 높일 수 있음.
후기
사실 2022년 하반기에 진행한 Stylegan2을 활용한 프로젝트 글을 쓰다가 GAN 논문들을 읽었던 것들이 정리가 제대로 안돼있고, 알아보기가 힘들어서 한번더 보는김에 다시 GAN 논문들 정리를 시작하려고 글을 쓰기 시작한건데 역시... 논문은 너무어렵네여. 수식은 봐도봐도 이해하기가 어려운 것 같습니다. 그래서 여러 글을 참고해서 이해하려고 노력하고 이해를 도우려고 노력해봤습니다. 다음으로는 GAN 구현을 가볍게 해보도록 하겠습니다.