1. 서론
http://ki-it.com/xml/40725/40725.pdf
클래스 불균형 데이터 분류 예측을 위한 클러스터 기반 언더샘플링 기법 (2024)
신용카드 사기 탐지나 장애 탐지 등 이상 탐지 분야에서는 다수클래스와 소수클래스가 불균형하게 분포하며 분류예측 성능에 많은 오류를 야기합니다. 해당 논문에서는 Kullback-Leibler Divergence을 활용하여 다수클래스의 모집단 분포를 반영하는 Cluster 기반 언더샘플링 방법을 제안했습니다. 이 방법은 다수클래스 데이터와 확률분포가 가장 유사한 샘플을 추출함으로써 언더샘플링의 주요 단점인 정보손실을 최소화합니다.
2. 본문
기존의 언더샘플링 기법은 다수클래스와 소수클래스 분포에 따라 데이터 축약의 효과가 미미하거나, 대표성이 떨어져 오히려 성능이 떨어지는 경우가 많습니다. 해당 논몬의 연구는 정보손실을 최소화하고 불균형 데이터의 분류예측 성능을 높이는데 우수한 방법인 클러스터 기반의 알고리즘을 진행하고 각 군집에서 층화추출법(Stratified random sampling)으로 샘플링하여 표본의 대표성을 향상시키고자 합니다.
전체적인 단계는 다음과 같습니다.

1. Original 불균형 데이터에서 train 데이터를 분리하고 이 중 다수클래스(y=0) 만으로 k-means cluster를 수행합니다.
2. (1)에서 얻어진 cluster를 기준으로 층화추출 샘플링을 진행하여 여러 subset을 얻습니다.
3. (2)의 subset 중 train 데이터의 쿨백-라이블러 발산 값을 계산하고 가장 작은 값을 갖는 subset을 최종 샘플로 결정합니다.
4. 소수클래스 데이터와 (3)으로부터 얻은 최종 샘플을 결합하여 균형데이터를 만듭니다.
5. 분류모델에 적합시킨 후 Test 데이터를 통해 성능을 평가합니다.
논문에서 제시한 쿨백 라이블러 발산 식은 다음과 같습니다.

모집단과 샘플 데이터의 mu(모집단 평균)과 sigma(공분산 행렬)을 비교하여 두 분포의 차이를 나타내는 지표로 사용합니다.
3. Credit Card Fraud Detection 데이터 실험
https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud
Credit Card Fraud Detection
Anonymized credit card transactions labeled as fraudulent or genuine
www.kaggle.com
논문에서는 제안한 CSSMC 방법론을 실증 데이터로 평가하였습니다. 불균형 데이터를 가장 쉽게 접할 수 있는 카드사기 분야를 선택하였고, kaggle의 ‘creditcard’ 데이터를 활용하였습니다.
데이터 : 학습에 사용한 데이터는 정상 199,020, 사고 344개로 불균 형비는 약 1:580이고,
모델 : LGBMClassfier
클러스터 : 15개
샘플 수 : 20,000개 (층화추출)
알고리즘과 미세조정 등의 영향을 통제한 상황에서의 샘플링 성능을 평가하고자 하는 것이 목적이므로, LGB모형과 하이퍼파라미터를 동일하게 사용하였으며, CSSMC의 cluster와 샘플 수는 각각 15, 20,000으로 설정하였고 그 결과는 아래 표 6과 같습니다.

선정된 Subset은 KLD 값을 4.2의 값이 선정됐고, F1-score 기준 0.81의 성능을 달성했습니다. 실제 논문 구현을 통해 실험을 진행해본 결과, 전체 데이터로 학습했을 때에 비해 0.03정도의 성능 향상을 이뤄냈습니다.
4. 의의
기존 7개의 언더샘플링 방법론과 모집단을 잘 반영할 수 있도록 설계된 3개의 연구방법을 다양한 불균형 실험데이터 셋으로 성능평가를 진행한 결과, 제안하는 CSSMC의 성능이 우수함을 확인할 수 있었습니다.
이러한 결과는 쿨백-라이블러 발산을 통해 샘플데이터와 모집단 분포의 유사도를 정량적으로 측정한 분석 결과라는 점에서 의의를 갖습니다. 쿨 백-라이블러 발산값은 모델 예측에 사용할 최종 샘플을 후보 샘플들 사이에서 선택하는데 판단 근거로 사용될 수 있는데, 사전 검증 절차를 통해 샘플에 대한 확신을 가지고 모델 수정 등의 절차만 반복할 수 있으므로 만족할 만한 성능이 확보되지 않은 경우 샘플링부터 다시 해야 하는 번거로움을 줄여 줄 수 있습니다.
5. 논문 구현
https://github.com/moonjoo98/FDS/tree/main/Data-level
FDS/Data-level at main · moonjoo98/FDS
FDS 리서치 및 구현. Contribute to moonjoo98/FDS development by creating an account on GitHub.
github.com
해당 깃허브 위치에 논문 구현 코드를 올려뒀습니다.
데이터셋 로드 및 전처리
앞선 링크의 캐글 Credit 데이터를 다운받아서 사용하시면 되고 코드는 다음과 같습니다.
1. zip파일을 data 경로에 해제하고 csv 파일로 불러옵니다.
df = pd.read_csv('./data/creditcard.csv',sep=',')
y = df['Class']
X = df.drop(["Class",'Time'], axis=1)
2. Amount 컬럼이 다른 컬럼과 스케일이 다르기 때문에 StandardScaler 적용해줍니다.
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_train_scaled_df = pd.DataFrame(X_train_scaled, columns=X_train.columns, index=X_train.index)
X_test_scaled = scaler.transform(X_test)
X_test_scaled_df = pd.DataFrame(X_test_scaled, columns=X_train.columns, index=X_test.index)여기서 주의할 점은 test 데이터에 transform만 적용하여 평가 데이터의 정보를 반영하여 스케일링을 하지 않도록 해야합니다. (data leakage)
3. 다수클래스 만으로 Kmeans Clustering을 수행하고, 얻어진 Cluster를 기준으로 층화 추출을 진행하여 여러 subset을 저장합니다.
논문에서 제안한 15개의 클러스터, 그리고 20,000개의 샘플을 만들기 위해 n_clusters = 15, total_sample-Size는 20,000으로 동일하게 구현했습니다.
X_majority = X_train_scaled_df[y_train == 0]
y_majority = y_train[y_train == 0]
# 2. k-means 클러스터링
n_clusters = 15 # 클러스터 개수를 15로 설정합니다.
kmeans = KMeans(n_clusters=n_clusters, random_state=42).fit(X_majority)
clusters = kmeans.predict(X_majority)
cluster_data_list = [X_majority[clusters == i] for i in range(n_clusters)]
cluster_sizes = [len(cluster_data) for cluster_data in cluster_data_list]
# 3. 여러 개의 랜덤 서브셋 생성
num_subsets = 10 # 생성할 서브셋의 개수
total_sample_size = 20000 # 총 샘플 수
all_sampled_subsets = []
def sample_without_replacement(cluster_data, n_samples, used_indices):
available_indices = list(set(range(len(cluster_data))) - used_indices)
if len(available_indices) < n_samples:
n_samples = len(available_indices)
sampled_indices = np.random.choice(available_indices, size=n_samples, replace=False)
used_indices.update(sampled_indices)
return cluster_data.iloc[sampled_indices]
for _ in range(num_subsets):
remaining_samples = total_sample_size
final_sampled_subset = pd.DataFrame()
used_indices_list = [set() for _ in range(n_clusters)]
while remaining_samples > 0:
for i, cluster_data in enumerate(cluster_data_list):
if remaining_samples <= 0:
break
available_samples = len(cluster_data) - len(used_indices_list[i])
if available_samples > 0:
if cluster_sizes[i] < 1300:
n_samples = available_samples
else:
n_samples = min(1300, available_samples, remaining_samples)
sampled_data = sample_without_replacement(cluster_data, n_samples, used_indices_list[i])
final_sampled_subset = pd.concat([final_sampled_subset, sampled_data])
remaining_samples -= n_samples
if len(final_sampled_subset) >= total_sample_size:
final_sampled_subset = final_sampled_subset.iloc[:total_sample_size]
remaining_samples = 0
break
all_sampled_subsets.append(final_sampled_subset)
4. all_sampled_subsets에 대해 쿨백-라이블러 발산값을 계산하고, 가장 작은 값을 갖는 best_subset을 선정한 다음 소수 클래스 데이터인 X_minority와 결합하여 균형 데이터로 만듭니다.
from numpy.linalg import slogdet, inv
import numpy as np
def kl_divergence(mu_p, sigma_p, mu_q, sigma_q):
"""
Calculate the KL divergence between two multivariate Gaussian distributions.
Parameters:
mu_p (np.ndarray): Mean vector of the distribution p
sigma_p (np.ndarray): Covariance matrix of the distribution p
mu_q (np.ndarray): Mean vector of the distribution q
sigma_q (np.ndarray): Covariance matrix of the distribution q
Returns:
float: The KL divergence D_KL(p || q)
"""
D = mu_p.shape[0] # Dimension of the distributions
# Calculate the determinant and inverse of sigma_q
det_sigma_p = np.linalg.det(sigma_p)
det_sigma_q = np.linalg.det(sigma_q)
inv_sigma_q = np.linalg.inv(sigma_q)
# Calculate the first term: 0.5 * log(det_sigma_q / det_sigma_p)
term1 = 0.5 * np.log(det_sigma_q / det_sigma_p) # 두 분포의 공분산 행렬의 행렬식 비율의 로그. 공분산 행렬의 행렬식은 분포의 "확산 정도"를 나타내므로, 두 분포의 확산 정도 차이를 로그 비율
# Calculate the second term: -D/2
term2 = -0.5 * D # 분포의 차원 D에 대한 조정 항, KL 발산 값이 분포의 차원에 대해 조정
# Calculate the third term: 0.5 * trace(inv_sigma_q @ sigma_p)
term3 = 0.5 * np.trace(inv_sigma_q @ sigma_p) # 분포 q의 공분산 행렬의 역행렬과 분포 p의 공분산 행렬의 곱의 대각합 공분산 행렬의 곱의 대각합은 두 분포의 상관 관계와 분산의 차이
# Calculate the fourth term: 0.5 * (mu_p - mu_q).T @ inv_sigma_q @ (mu_p - mu_q)
diff_mu = mu_p - mu_q
term4 = 0.5 * diff_mu.T @ inv_sigma_q @ diff_mu # 두 분포의 평균 벡터 차이에 대한 조정 항, @는 행렬 곱셈 연산자, 이 항은 두 분포의 중심(평균 벡터)의 차이를 측정합니다. 두 분포의 평균 벡터가 얼마나 다른지.
# Sum all the terms to get the KL divergence
kl_div = term1 + term2 + term3 + term4
return kl_div
kl_divergences = []
mu_p = X_majority.mean().values
sigma_p = np.cov(X_majority, rowvar=False) # 원본 데이터의 공분산 행렬
for subset in all_sampled_subsets:
mu_q = subset.mean().values
sigma_q = np.cov(subset, rowvar=False) # Subest의 공분산 행렬
kl_divergences.append(kl_divergence(mu_p, sigma_p, mu_q, sigma_q)) # 원본 데이터와 subset의 mu(모집단 평균)와 sigma(공분산 행렬) 비교
# 5. 최적 subset 선택
best_subset_idx = np.argmin(kl_divergences)
best_subset = all_sampled_subsets[best_subset_idx]
X_minority = X_train_scaled_df[y_train == 1]
y_minority = y_train[y_train == 1]
X_balanced = pd.concat([X_minority, best_subset])
y_balanced = pd.concat([y_minority, pd.Series([0]*len(best_subset))])
5. LGBMClassfier로 적합하여 전체 데이터 X_train과 언더샘플링 데이터 X_balanced의 성능 비교.
def evaluate(model):
model.fit(X_train,y_train)
pre = model.predict(X_test)
accuracy = accuracy_score(pre,y_test)
precision = precision_score(pre,y_test)
recall = recall_score(pre,y_test)
f1 = f1_score(pre,y_test)
sns.heatmap(confusion_matrix(pre,y_test),annot=True)
print(model)
print('Accuracy : ',accuracy,'Recall : ',recall, "Precision : ",precision,"F1 : ",f1)
clf = lgb.LGBMClassifier(random_state=42)
clf.fit(X_train, y_train)
evaluate(clf)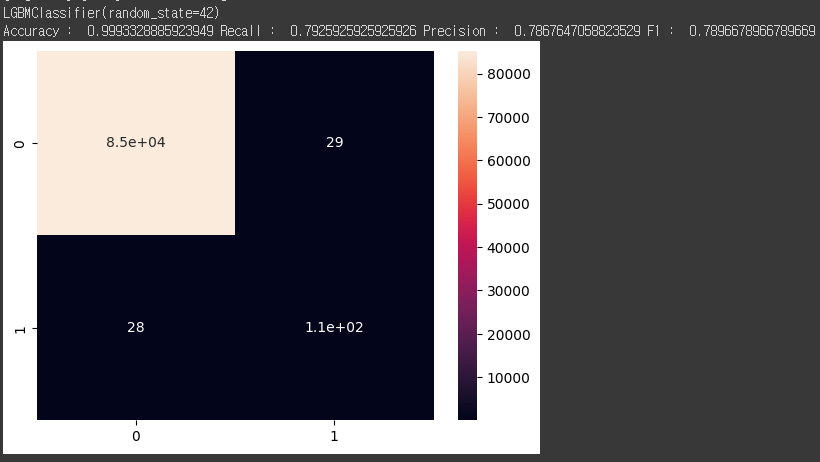
clf = lgb.LGBMClassifier(random_state=42)
clf.fit(X_balanced, y_balanced)
pre = clf.predict(X_test)
accuracy = accuracy_score(pre,y_test)
precision = precision_score(pre,y_test)
recall = recall_score(pre,y_test)
f1 = f1_score(pre,y_test)
sns.heatmap(confusion_matrix(pre,y_test),annot=True)
print(clf)
print('Accuracy : ',accuracy,'Recall : ',recall, "Precision : ",precision,"F1 : ",f1)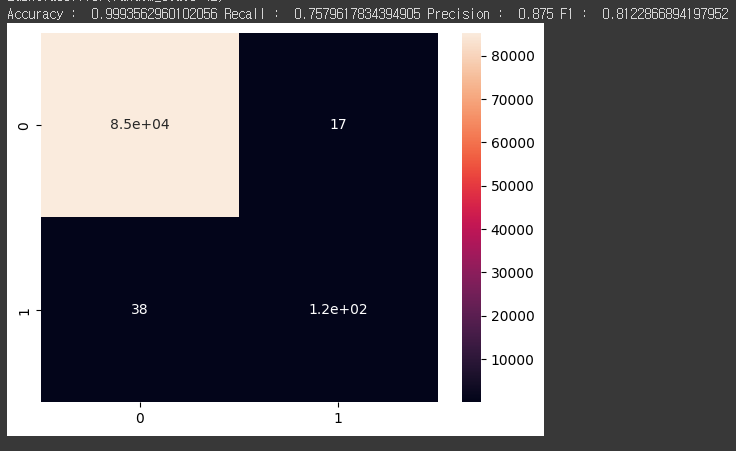
논문에서 제안한 CSSMC 방법이 전체 데이터로 학습한 것에 비해 약 0.02정도 성능이 더 높은 것을 확인하실 수 있습니다.
6. 결론
논문에서 실험한 결과와 동일한 성능이 나왔고, 실제로 전체 데이터로 학습한 것에 비해 성능이 높아지는 것을 확인할 수 있었습니다. 그러나, RandomForest 분류 모델에 적합했을 땐, 전체 데이터의 성능이 언더샘플링한 데이터보다 성능이 높았기 때문에 상황에 따라 적절히 사용하는 것이 필요합니다.
'ML' 카테고리의 다른 글
| [ML] 시계열 데이터 - 특징, 정상성 / 비정상성, ACF, PACF, ADF (1) | 2024.07.05 |
|---|---|
| [ML] 머신러닝 기초 (5) Linear Regression. 회귀 실습 (0) | 2024.02.19 |
| [ML] 머신러닝 기초 (4) Linear Regression 회귀 이론 (0) | 2024.02.15 |
| [ML] 머신러닝 기초 (3) 머신러닝 기본 수학 이론 (1) | 2024.02.14 |
| [ML] 머신러닝 기초 (2) 머신러닝 기본 용어 정리 (1) | 2024.01.31 |