https://mz-moonzoo.tistory.com/52
[ML] 머신러닝 기초 (4) Linear Regression 회귀 이론
https://mcode.co.kr/video/list2?viewMode=view&idx=21 메타코드M 빅데이터 , AI 강의 플랫폼 & IT 현직자 모임 플랫폼ㅣ메타코드 커뮤니티 일원이 되시기 바랍니다. mcode.co.kr 이전 ML 카테고리의 포스팅에 이어
mz-moonzoo.tistory.com
선형 회귀의 이론을 포스팅하고 실습 강의 리뷰는 굳이 하지 않으려했지만 간단하게 코드 리뷰를 해보겠습니다.
실습 강의 및 코드는 메타코드 링크에서 받아보실 수 있습니다.
https://mcode.co.kr/video/list2?viewMode=view&idx=21
메타코드M
빅데이터 , AI 강의 플랫폼 & IT 현직자 모임 플랫폼ㅣ메타코드 커뮤니티 일원이 되시기 바랍니다.
mcode.co.kr
이번 글에서는 선형 회귀 모델 실습에 대한 코드와 다중 회귀 모델 과제에 대한 코드 리뷰를 동시에 진행하겠습니다.
Linear_Regression_Answer 리뷰
단순 선형 회귀 모델을 최소제곱법과 경사하강법(Gradient Descent)을 사용하여 학습하는 과정을 구현했습니다.
이 코드에서는 가상의 데이터를 생성하고 이를 통해 모델을 학습시키는 전체 과정을 포함하고 있습니다.
1. 데이터 준비
데이터 생성

X = np.arange(-200, 200): -200부터 199까지의 정수를 생성하여 입력 데이터 X를 만듭니다.
delta와 gamma는 각각 -50에서 50, -30에서 30 사이의 균일 분포를 따르는 무작위 값을 가지며, 이는 데이터에 노이즈를 추가하여 실제와 같은 데이터 패턴을 만듭니다.
y = 0.5*X + 13 + delta - gamma: 이는 를 계산하는 실제 함수로, 에 대한 선형 관계에 노이즈를 추가하여 값을 생성합니다.
학습 데이터 / 평가 데이터 분할

train_test_split(X, y, test_size=0.2, random_state=42): 생성된 데이터를 학습 데이터와 평가 데이터로 분할합니다. 여기서 test_size=0.2는 전체 데이터의 20%가 테스트 데이터로 사용됨을 의미하며, random_state는 데이터 분할 시 무작위성을 제어합니다.
학습 데이터와 평가 데이터의 산점도를 보시면 비슷한 분포로 보입니다.
2. numpy 라이브러리를 활용해 선형 회귀 모델 구현
최적의 선형 회귀 모델을 찾기 위해 MSE(Mean Squared Error) 손실을 최소화하도록 학습을 진행하겠습니다.
최적의 모델은 모든 데이터에 대해 실제값과 예측값의 차이가 제일 작은 모델 즉, MSE loss를 최소화한 모델입니다.
MSE loss와 경사 하강법(Gradient Descent)을 numpy로 구현하여 선형 회귀 모델을 학습하는 과정을 구현했습니다.

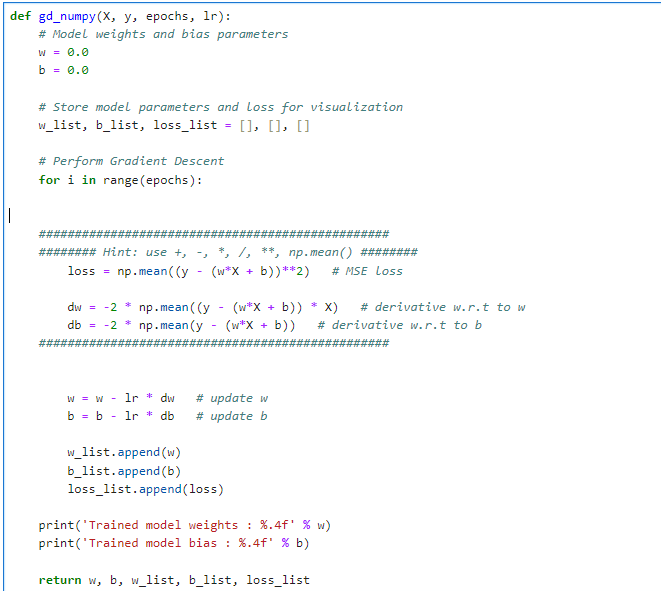
이 함수는 입력 데이터 X, 타겟 데이터 , 반복 횟수(epochs), 그리고 학습률(lr)을 인자로 받습니다. 학습 과정에서 모델의 가중치와 편향을 최적화하여 데이터의 선형 관계를 가장 잘 나타내는 선을 찾습니다.
모델 초기화:
- w와 b는 각각 모델의 가중치와 편향을 나타냅니다. 초기값은 0.0으로 설정됩니다.
- w_list, b_list, loss_list는 학습 과정에서 각각의 가중치, 편향, 손실 값을 저장하기 위한 리스트입니다.
경사 하강법 실행:
- 지정된 epochs만큼 반복하면서 가중치와 편향을 업데이트합니다.
- 손실 계산: 평균 제곱 오차(Mean Squared Error, MSE)를 사용해 모델의 손실을 계산합니다. 이는 모델 예측값과 실제 값 사이의 차이의 제곱의 평균입니다.
- 가중치 및 편향의 그래디언트 계산: 손실 함수의 가중치(w)와 편향(b)에 대한 미분을 계산하여, 어떻게 w와 b를 조정해야 손실을 줄일 수 있는지 결정합니다.
- 파라미터 업데이트: 계산된 그래디언트와 학습률(lr)을 사용하여 w와 b를 업데이트합니다. 학습률은 업데이트의 크기를 조절하는데, 너무 크면 학습이 불안정해지고, 너무 작으면 학습 속도가 느려집니다.
결과 저장 및 출력:
- 각 반복마다 업데이트된 가중치, 편향, 그리고 계산된 손실 값을 리스트에 추가합니다. 이를 통해 학습 과정을 시각화하고 분석할 수 있습니다.
- 학습이 완료된 후 최종 모델의 가중치와 편향을 출력합니다.
반환 값:
- 학습이 끝난 후, 최종적으로 업데이트된 가중치 w, 편향 b와 함께, 학습 과정에서 기록한 가중치, 편향, 손실의 리스트를 반환합니다. 이 데이터를 사용하여 학습 과정을 시각화하거나 분석할 수 있습니다.
가중치와 편향을 미분하는 주된 이유는 모델의 학습 과정에서 손실 함수(loss function)의 최소값을 찾기 위해서입니다. 손실 함수는 모델의 예측값과 실제값 사이의 차이를 수치화한 것으로, 이 값을 최소화하려는 것이 학습의 목표입니다. 가중치(weight)와 편향(bias)은 모델이 데이터를 어떻게 해석하고 예측을 수행하는지 결정하는 핵심 파라미터입니다.
미분의 역할:
1. 방향과 크기 결정: 손실 함수의 가중치와 편향에 대한 미분(그래디언트)은 해당 파라미터를 조정해야 할 방향과 크기를 제공합니다. 즉, 손실을 줄이기 위해 각 파라미터를 증가시켜야 할지 감소시켜야 할지, 그리고 얼마나 조정해야 하는지를 알려줍니다.
2. 손실 최소화: 그래디언트는 손실 함수의 기울기를 나타냅니다. 손실 함수의 최소점에서는 이 기울기가 0에 가까워집니다. 경사 하강법(Gradient Descent)은 이 기울기(그래디언트)를 사용하여 반복적으로 파라미터를 업데이트함으로써 손실 함수의 최소값을 찾습니다.
3. 효율적인 학습: 가중치와 편향을 적절히 미분하고 업데이트함으로써, 모델은 더 정확한 예측을 할 수 있게 되고, 학습 과정이 효율적으로 이루어집니다. 이는 과대적합(overfitting)이나 과소적합(underfitting)을 방지하고, 모델의 일반화 능력을 향상시킬 수 있습니다.
gd_numpy 함수로 학습 진행
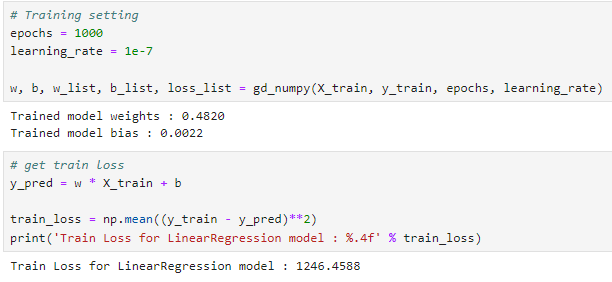
이 코드는 선형 회귀 모델의 학습을 진행하여 학습 시의 손실(train loss)을 계산하고 출력하는 과정을 나타냅니다.
선형 회귀 모델은 입력 데이터 와 타겟 데이터 사이의 선형 관계를 모델링하여, 새로운 입력 데이터에 대한 예측값을 제공합니다. 이 과정에서 모델의 성능을 평가하기 위해 훈련 손실을 계산합니다.
y_pred = w * X_train + b: 모델의 예측값(y_pred)을 계산합니다. 여기서 w는 모델의 가중치, b는 편향, X_train은 훈련 데이터의 입력 변수입니다. 모델의 예측값은 입력 데이터 X_train에 대한 선형 함수로, 각 입력 데이터 포인트에 대해 가중치 w를 곱하고 편향 b를 더해 계산됩니다.
train_loss = np.mean((y_train - y_pred)**2): 훈련 데이터에 대한 손실을 계산합니다. 손실은 실제 타겟 데이터 y_train과 모델의 예측값 y_pred 사이의 차이(오차)를 제곱하여 평균을 낸 값입니다. 이는 평균 제곱 오차(Mean Squared Error, MSE)라고 하며, 회귀 모델의 성능 평가 지표로 널리 사용됩니다. MSE는 모델의 예측이 얼마나 실제 값에 가까운지를 수치적으로 나타내며, 값이 작을수록 모델의 성능이 좋다고 평가할 수 있습니다.
평가 데이터에 대한 예측 결과
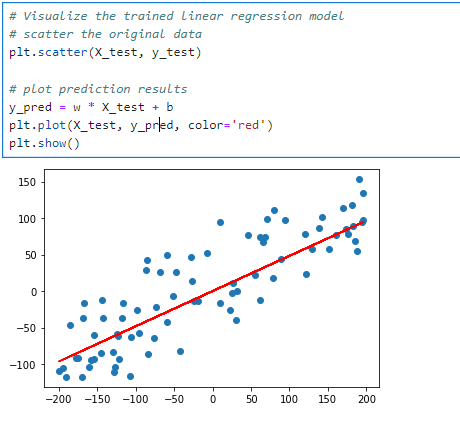

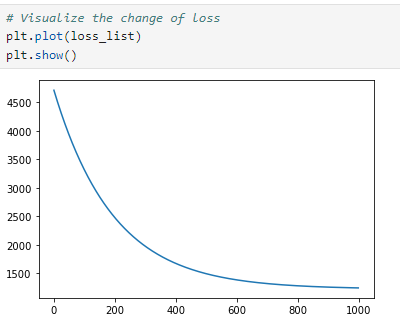
여기선 1447.9247의 test_loss가 나왔습니다.
loss의 크기가 높게 나오는 것 같지만 epochs가 반복될 수록 loss가 줄어드는 것을 확인할 수 있습니다.
이 수치를 기준으로 이 후에는 sklearn 라이브러리에서 제공하는 최소제곱법을 적용한 선형 회귀 모델과 경사하강법을 적용한 선형 회귀 모델을 비교해보도록 하겠습니다.
3. sklearn 라이브러리 LinearRegression 모델로 최적의 선형 회귀 모델 구현
sklearn 라이브러리의 LinearRegression 모델은 경사하강법 대신 최소제곱법(Least Squares Method)를 사용해 학습을 진행합니다. 그렇다면 경사하강법과 최소제곱법의 차이는 무엇일까요? 간단히 차이점을 짚고 넘어가겠습니다.
경사 하강법 (Gradient Descent)
- 장점:
- 대규모 데이터셋에 적합: 데이터의 크기가 매우 클 때 효율적으로 사용할 수 있습니다.
- 유연성: 비선형 회귀를 포함하여 다양한 종류의 손실 함수에 적용할 수 있습니다.
- 단점:
- 수렴 속도: 적절한 학습률을 선택하지 않으면 수렴 속도가 느려질 수 있습니다.
- 최적화가 보장되지 않음: 잘못된 초기값이나 학습률 설정으로 인해 지역 최소값(local minima)에 빠질 수 있습니다(선형회귀의 경우 볼록 함수이기 때문에 이 문제는 크게 걱정하지 않아도 됩니다).
최소제곱법 (Least Squares Method)
- 장점:
- 완벽한 해: 데이터에 대한 선형 회귀 모델의 파라미터를 직접 계산할 수 있으며, 계산된 해는 전역 최소값(global minimum)입니다.
- 계산 효율성: 작거나 중간 크기의 데이터셋에서 매우 빠르게 결과를 얻을 수 있습니다.
- 단점:
- 계산 복잡성: 특성의 수가 많을 경우, (X^T X)^{-1} 역행렬 계산에 큰 계산 비용이 들 수 있습니다. 특성의 수가 매우 많거나 데이터셋이 매우 클 경우 메모리 부족이나 성능 저하를 초래할 수 있습니다.
- 비선형 모델에 적용 불가: 최소제곱법은 선형 회귀 모델에는 잘 작동하지만, 비선형 관계를 모델링하는 경우에는 사용할 수 없습니다.
결론
- 데이터 크기와 특성의 수: 작거나 중간 크기의 데이터셋에는 최소제곱법이 더 빠르고 효율적일 수 있습니다. 대규모 데이터셋이나 특성의 수가 많은 경우, 경사 하강법이 더 적합할 수 있습니다.
- 모델의 복잡성: 선형 모델에는 최소제곱법이 적합할 수 있지만, 비선형 회귀 모델이나 복잡한 손실 함수를 사용하는 경우 경사 하강법이 더 유연합니다.
lr_sklearn 함수로 학습 진행
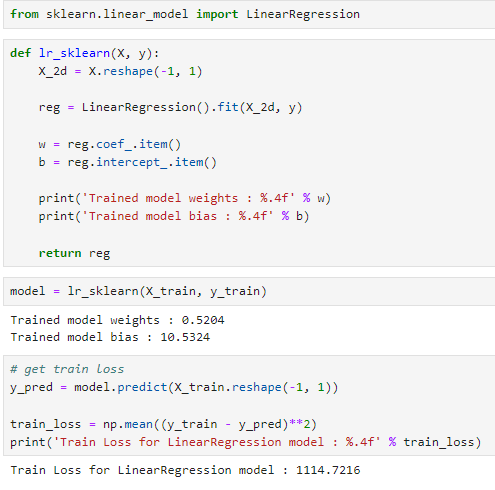
lr_sklearn 함수
- 데이터 형태 조정: 입력 데이터 X를 선형 회귀 모델이 요구하는 2차원 형태로 변환합니다. X.reshape(-1, 1)을 통해 X를 열 벡터로 만듭니다. -1은 해당 차원의 크기를 자동으로 계산하라는 의미입니다.
- 선형 회귀 모델 학습: LinearRegression().fit(X_2d, y)를 사용하여 모델을 훈련 데이터에 맞춥니다. 이 과정에서 모델은 최소제곱법을 사용하여 가중치(w)와 편향(b)을 학습합니다.
- 학습된 모델 파라미터 추출: 학습된 모델의 가중치(coef_)와 편향(intercept_)을 추출합니다. item()을 사용하여 numpy 배열에서 스칼라 값을 얻습니다.
- 모델 파라미터 출력: 학습된 가중치와 편향을 출력합니다.
- 모델 반환: 학습된 선형 회귀 모델 객체를 반환합니다.
훈련 손실 계산
- y_pred = model.predict(X_train.reshape(-1, 1)): 학습된 모델을 사용하여 훈련 데이터 X_train에 대한 예측값 y_pred를 계산합니다. X_train도 2차원 형태로 변환해야 합니다.
- train_loss = np.mean((y_train - y_pred)**2): 예측값과 실제 훈련 데이터 타겟 y_train 사이의 평균 제곱 오차(Mean Squared Error, MSE)를 계산하여 훈련 손실을 구합니다.
평가 데이터에 대한 예측 결과
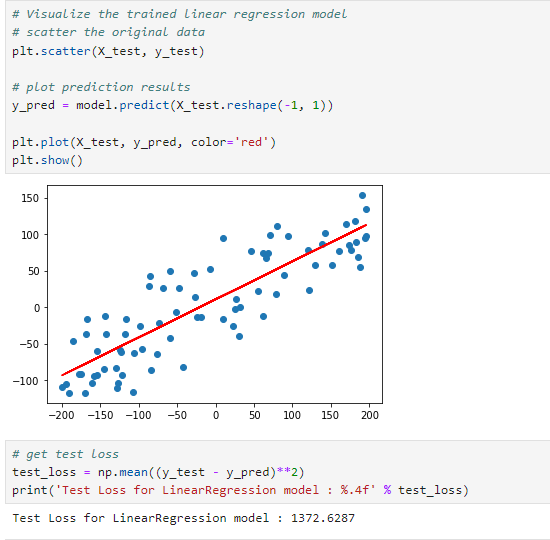
model.predict(X_test.reshape(-1,1)) : 테스트 데이터에 대한 예측 값을 계산합니다.
test_loss = np.mean((y_test - y_pred)**2): 평가 데이터의 예측값과 실제 평가 데이터의 값인 y_test 사이의 평균 제곱 오차(Mean Squared Error, MSE)를 계산하여 훈련 손실을 구합니다.
여기서의 test loss는 1372.6287로 경사하강법을 적용한 선형회귀 모델보다 loss가 낮은 것을 확인할 수 있습니다.
그러므로 특성(피처)가 적을 경우 경사하강법보다 최소제곱법을 적용하는 것이 좋을 수 있습니다.
4. sklearn 라이브러리의 SGDRegression 모델을 활용해 최적의 선형 회귀 모델 찾기
앞선 2번에서는 경사하강법을 직접 구현하였으나, sklearn 라이브러리를 사용하면, 별도의 gradient 계산 없이 모델을 쉽게 학습시킬 수 있습니다. 아래 코드는 Scikit-learn 라이브러리를 사용하여 확률적 경사 하강법(Stochastic Gradient Descent, SGD)을 이용한 선형 회귀 모델을 학습시키고, 훈련 및 테스트 데이터에 대한 손실을 계산하는 과정을 구현한 것입니다.
gd_sklearn로 학습 진행
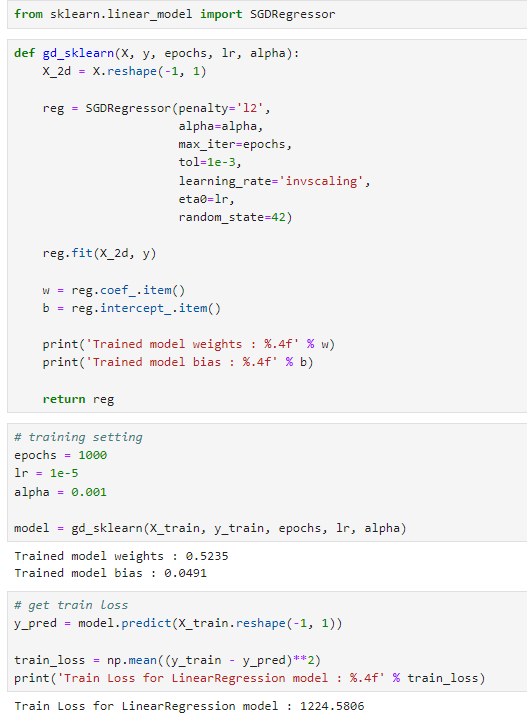
gd_sklearn
- 데이터 형태 조정: 입력 데이터 X를 선형 회귀 모델이 요구하는 2차원 형태로 변환합니다(X.reshape(-1, 1)).
- SGDRegressor 설정 및 학습:
- SGDRegressor는 선형 모델을 SGD를 사용하여 최적화하는 클래스입니다.
- penalty='l2'는 L2 규제를 사용함을 나타냅니다. 이는 과대적합을 방지하고 모델의 일반화 능력을 향상시키는 데 도움을 줍니다.
- alpha는 L2 규제의 강도를 조절합니다. 높은 값은 더 강한 규제를 의미합니다.
- max_iter=epochs는 최대 반복 횟수를 지정합니다.
- tol=1e-3는 알고리즘이 수렴으로 판단하는 기준입니다.
- learning_rate='invscaling'는 학습률이 반복에 따라 어떻게 조정되는지를 정의합니다. 'invscaling'은 반복 횟수의 함수로 학습률을 감소시킵니다.
- eta0=lr는 초기 학습률을 설정합니다.
- random_state=42는 결과의 재현성을 위해 난수 생성기의 시드를 고정합니다.
- reg.fit(X_2d, y)는 모델을 학습 데이터에 적합시킵니다.
- 학습된 모델 파라미터 추출: coef_와 intercept_ 속성에서 학습된 가중치와 편향을 추출합니다.
- 모델 파라미터 출력: 학습된 가중치와 편향을 출력합니다.
훈련 손실 계산:
- y_pred = model.predict(X_train.reshape(-1, 1))를 사용하여 훈련 데이터에 대한 예측값을 계산합니다.
- np.mean((y_train - y_pred)**2)로 훈련 데이터에 대한 평균 제곱 오차(Mean Squared Error, MSE)를 계산하고 출력합니다.
평가 데이터에 대한 예측 결과
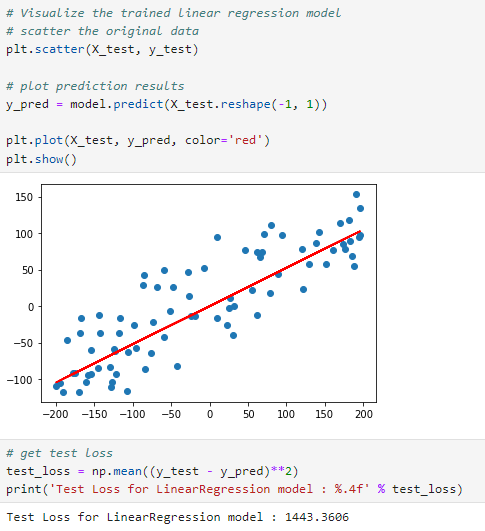
- y_pred = model.predict(X_test.reshape(-1, 1))를 사용하여 테스트 데이터에 대한 예측값을 계산합니다.
- np.mean((y_test - y_pred)**2)로 테스트 데이터에 대한 MSE를 계산하고 출력합니다.
test loss는 1443.3606으로 앞서 직접 경사하강법을 구현한 것과 크게 차이가 나지 않는 것을 확인하실 수 있습니다.
Polynomial_Regression_Answer 리뷰
이번에는 다항 회귀 모델을 위한 경사 하강법(Gradient Descent) 최적화 알고리즘을 구현해보겠습니다. 실습 과제로 내주신 것을 구현하고 코드에 대한 설명을 추가했습니다. 다항 회귀 모델은 입력 변수 의 다항식을 사용하여 출력 변수 를 예측합니다. 이 코드에서는 의 세제곱, 제곱, 그리고 자체를 포함하는 3차 다항식을 사용합니다.
1. 데이터 생성
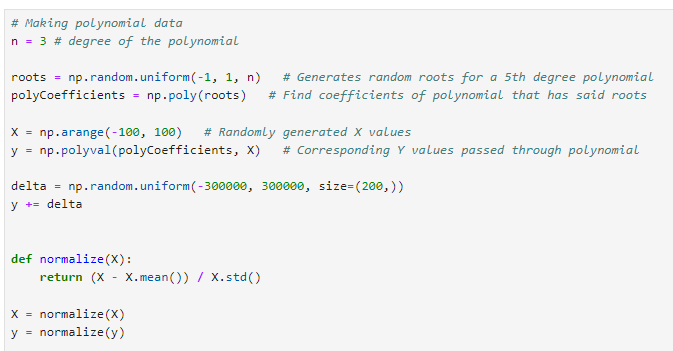
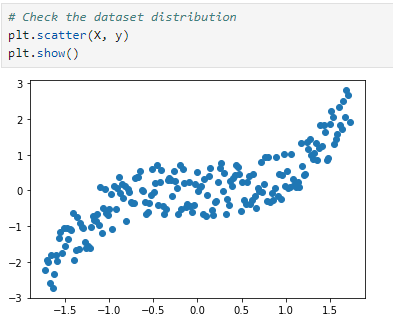
- 다항식의 근 생성: np.random.uniform(-1, 1, n)을 사용하여 -1과 1 사이에서 무작위로 n개의 근을 생성합니다. 여기서 n=3은 생성할 다항식의 차수입니다.
- 다항식 계수 계산: np.poly(roots) 함수를 사용하여 생성된 근으로부터 다항식의 계수를 계산합니다. 이 함수는 주어진 근들을 가지는 다항식의 계수를 반환합니다.
- 입력 데이터 X 생성: np.arange(-100, 100)을 사용하여 -100부터 99까지의 정수 배열을 생성합니다. 이 배열은 다항식의 입력값으로 사용됩니다.
- 출력 데이터 y 계산: np.polyval(polyCoefficients, X)을 사용하여 각 X 값에 대한 다항식의 출력값 y를 계산합니다. 계산된 y 값은 X에 해당하는 다항식의 값입니다.
- 노이즈 추가: y += delta를 사용하여 y 값에 노이즈를 추가합니다. 여기서 delta는 -300000과 300000 사이에서 무작위로 생성된 200개의 값으로, 실제 데이터에 존재할 수 있는 잡음을 모방하기 위해 사용됩니다.
데이터 정규화
- normalize(X) 함수는 주어진 데이터 배열 X의 평균을 빼고 표준편차로 나누어 정규화합니다. 이는 데이터의 평균을 0으로, 표준편차를 1로 조정하여 다양한 스케일의 데이터를 동일한 스케일로 만듭니다. 정규화는 학습 알고리즘이 더 빠르고 안정적으로 수렴하도록 돕습니다.
훈련 데이터와 테스트 데이터 분할
- train_test_split(X, y, test_size=0.2, random_state=42) 함수를 사용하여 생성 및 정규화된 데이터를 훈련 데이터와 테스트 데이터로 분할합니다. 여기서 test_size=0.2는 전체 데이터의 20%가 테스트 데이터로 사용됨을 의미하며, random_state=42는 데이터 분할 시 무작위성을 제어하여 결과의 재현 가능성을 보장합니다.
2. numpy 라이브러리를 통해, 최적의 다항 회귀 모델 학습
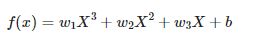
이 코드는 넘파이(Numpy)를 사용하여 3차 다항 회귀 모델을 경사 하강법(Gradient Descent)으로 학습하는 과정을 구현한 것입니다. 다항 회귀는 입력 변수 에 대해 비선형 관계를 모델링하는 회귀 분석의 한 형태로, 이 경우 의 3차, 2차, 1차 항을 사용합니다.
gd_numpy로 학습 진행
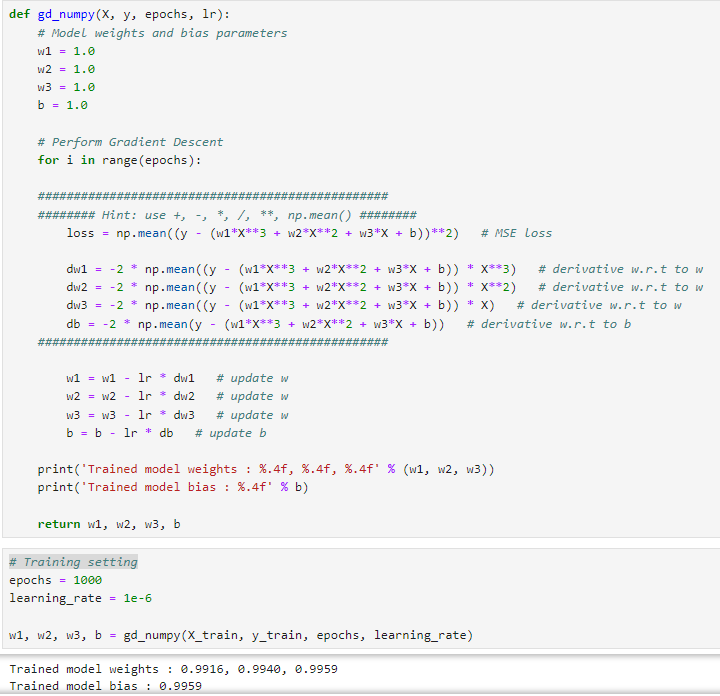
- 초기화: 가중치 w1, w2, w3와 편향 b를 1.0으로 초기화합니다.
- 경사 하강법 실행: 지정된 epochs 횟수만큼 반복합니다.
- 손실 계산: 평균 제곱 오차(Mean Squared Error, MSE)를 사용해 모델의 손실을 계산합니다. 이는 모델 예측값과 실제 값 사이의 차이의 제곱의 평균입니다.
- 그래디언트 계산: 손실 함수의 각 가중치(w1, w2, w3)와 편향(b)에 대한 미분을 계산합니다. 이는 손실을 최소화하는 방향으로 가중치와 편향을 조정하는 데 사용됩니다. 여기서 - 2는 MSE 손실 함수를 파라미터에 대해 미분할 때 자연스럽게 나오는 계수이며, 를 곱하는 것은 파라미터의 변화가 y의예측 값에 어떻게 영향을 미치는지를 나타내는 데 필요합니다.
- 파라미터 업데이트: 계산된 그래디언트와 학습률(lr)을 사용하여 가중치와 편향을 업데이트합니다.
- 가중치 및 편향 출력, 반환: 학습된 모델의 가중치(w1, w2, w3)와 편향(b)을 출력하고 반환합니다.
훈련 손실 계산
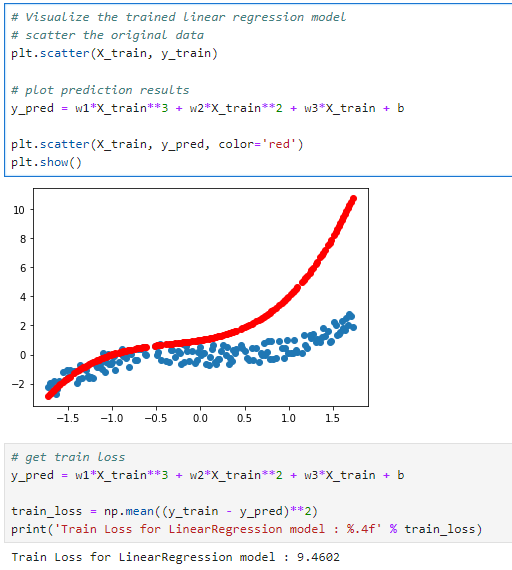
y_pred = w1*X_train**3 + w2*X_train**2 + w3*X_train + b: 훈련 데이터 X_train에 대한 모델의 예측값 y_pred를 계산합니다. 이 때, 각각의 계수 w1, w2, w3와 편향 는 모델 학습 과정에서 최적화된 파라미터입니다.
train_loss = np.mean((y_train - y_pred)**2): 훈련 데이터에 대한 평균 제곱 오차(Mean Squared Error, MSE)를 계산합니다. 이는 실제 타겟 값 y_train과 예측값 y_pred 사이의 차이의 제곱의 평균으로, 모델의 성능을 나타내는 지표 중 하나입니다.
평가 데이터에 대한 예측 결과
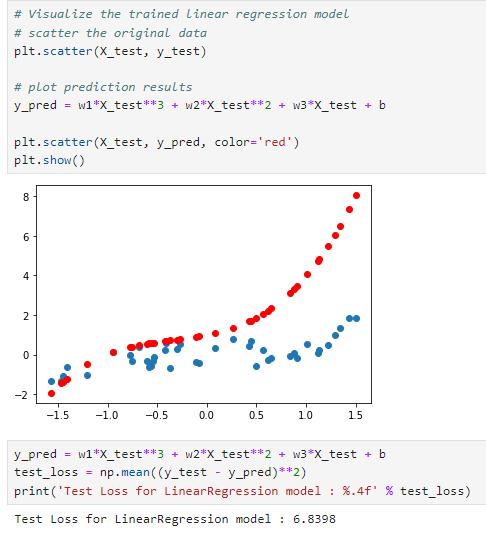
y_pred = w1*X_test**3 + w2*X_test**2 + w3*X_test + b: 테스트 데이터 X_test에 대한 모델의 예측값 y_pred를 계산합니다.
test_loss = np.mean((y_test - y_pred)**2): 테스트 데이터에 대한 MSE를 계산합니다. 이는 실제 타겟 값 y_test와 예측값 y_pred 사이의 차이의 제곱의 평균으로, 모델이 새로운 데이터에 대해 얼마나 잘 예측하는지를 평가하는 데 사용됩니다.
Test loss 는 6.8398로 실제 타겟값과 예측값이 비슷한 패턴을 띄고 있으나, 일관된 차이가 보이는 것을 산점도를 통해 보실 수 있습니다. 산점도에서 빨간색 점들은 모델이 예측한 값이고 파란색 점들은 실제 관측된 값입니다. 두 점 집합 사이의 거리는 모델의 예측 오류를 나타냅니다.
- 모델은 의 값이 증가함에 따라 값도 증가하는 비선형적인 패턴을 따르는 것으로 보입니다. 이는 모델이 3차 다항 회귀 모델임을 반영했기 때문입니다.
- 빨간색 점들(모델의 예측)은 축을 따라 증가하는 값의 패턴을 잘 따르고 있으나, 파란색 점들(실제 값)과 비교했을 때 일관된 오차가 존재합니다.
- 의 값이 작을 때(음수 포함)는 모델의 예측이 실제 값에 비교적 가깝지만, 의 값이 커질수록 모델의 예측과 실제 값 사이의 차이가 더욱 크게 벌어지는 것을 볼 수 있습니다. 이는 모델이 데이터의 전 범위에 걸쳐 동일한 정확도로 예측하지 못한다는 것을 나타냅니다.
이는 예측 오차가 증가하고 있음을 나타내며, 모델이 이 데이터의 비선형성을 완벽하게 학습하지 못했거나, 과소적합(Underfitting)의 문제가 있을 수 있음을 시사합니다.
3. sklearn 라이브러리를 통해, 최적의 다항 회귀 모델 학습
이 코드는 sklearn 라이브러리의 LinearRegression에 다항식 특징으로 다항 선형회귀 모델을 학습해보도록 하겠습니다.
주어진 학습 데이터 X_train과 y_train을 사용하여 다항 회귀 모델을 학습시키고, 학습된 모델의 성능을 시각화하며, 손실을 계산하는 과정을 구현합니다.
gd_sklearn 학습 진행
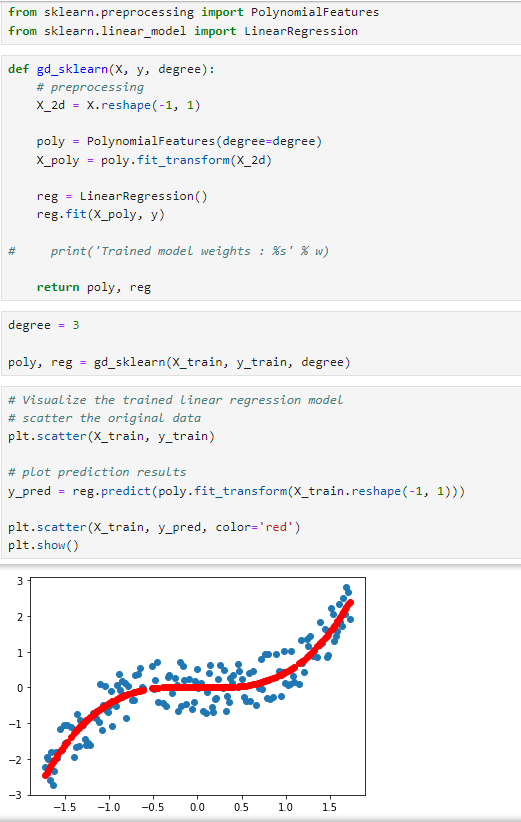
gd_sklearn
- gd_sklearn 함수는 입력 데이터 X, 타겟 데이터 y, 그리고 다항식의 차수 degree를 인자로 받습니다.
- X 데이터는 2차원 배열로 재구성됩니다. (X.reshape(-1, 1))
- PolynomialFeatures를 사용하여 주어진 degree에 대한 다항식 특징을 생성합니다. 이를 통해 선형 회귀 모델이 더 복잡한 비선형 관계를 학습할 수 있게 됩니다.
- LinearRegression 객체를 생성하고, 변환된 다항식 특징 X_poly와 타겟 y를 사용하여 모델을 학습시킵니다.
- 학습된 다항 회귀 모델과 변환 객체 poly를 반환합니다.
다항 회귀 모델 학습
- degree = 3는 다항식의 차수를 3으로 설정합니다.
- gd_sklearn 함수를 호출하여 훈련 데이터에 대한 다항 회귀 모델을 학습시킵니다.
모델 시각화
- plt.scatter(X_train, y_train)는 훈련 데이터의 실제 타겟 값을 파란색 점으로 산점도에 표시합니다.
- y_pred = reg.predict(poly.fit_transform(X_train.reshape(-1, 1)))를 사용하여 학습된 모델로 훈련 데이터의 예측값을 계산합니다.
- plt.scatter(X_train, y_pred, color='red')는 모델의 예측값을 빨간색 점으로 산점도에 표시합니다.
- plt.show()로 그래프를 화면에 표시합니다.
훈련 손실 계산
- train_loss = np.mean((y_train - y_pred)**2)는 훈련 데이터에 대한 평균 제곱 오차(MSE)를 계산합니다. 이는 모델의 예측값과 실제값 사이의 차이의 제곱을 평균내어 얻습니다.
- print('Train Loss for LinearRegression model : %.4f' % train_loss)는 계산된 훈련 손실을 출력합니다.
평가 데이터에 대한 예측 결과
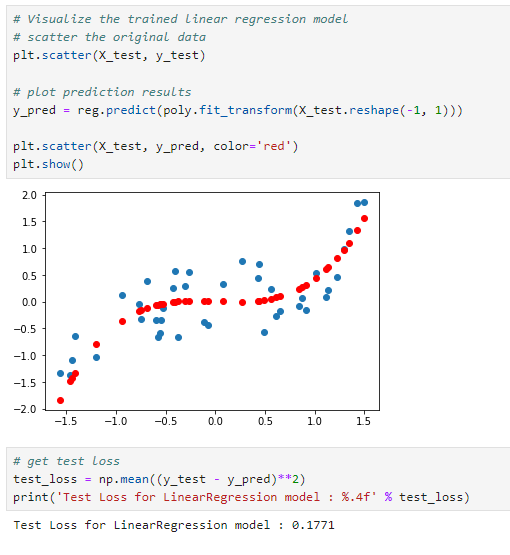
- plt.scatter(X_test, y_test): 테스트 데이터셋의 실제 � 값들을 산점도로 그립니다. 이들은 그래프에서 파란색 점으로 표현됩니다.
- y_pred = reg.predict(poly.fit_transform(X_test.reshape(-1, 1))): 훈련된 다항 회귀 모델을 사용하여 X_test에 대한 예측값 y_pred를 계산합니다. poly.fit_transform은 X_test 데이터를 다항식 특징으로 변환합니다, 이 과정은 학습할 때 사용된 동일한 다항 변환을 테스트 데이터에 적용하여 예측을 수행하기 위함입니다.
- plt.scatter(X_test, y_pred, color='red'): 모델의 예측값을 산점도에 빨간색 점으로 나타냅니다.
- plt.show(): 그래프를 화면에 표시합니다.
- test_loss = np.mean((y_test - y_pred)**2): 테스트 데이터셋에 대한 평균 제곱 오차(Mean Squared Error, MSE)를 계산합니다. 이는 모델의 예측값과 실제값 사이의 차이의 제곱을 평균낸 것으로, 모델의 예측 성능을 나타내는 지표입니다.
test loss는 0.1771로 numpy로 구현한 다항 회귀 모델의 loss에 비해 매우 낮은 loss를 보여줍니다.
산점도를 해석해보면,
- 파란색 점과 빨간색 점 사이의 수직 거리는 각 값에 대한 예측 오류를 나타냅니다. 이 거리가 작을수록 모델의 예측이 정확합니다.
- 축의 값이 증가함에 따라 축의 값도 증가하는 비선형 패턴을 보이며, 모델은 이 비선형 관계를 어느 정도 포착하고 있음을 나타냅니다.
- 전반적으로 빨간색 점들이 파란색 점들을 따라가고 있습니다. 이를 통해 완벽하지는 않으나 모델이 예측을 잘하고 있는것으로 생각할 수 있습니다.
numpy로 직접 구현한 다항 회귀 모델과 성능이 많이 차이나는 이유는 epochs, 학습률 등의 하이퍼파라미터, sklearn 모듈의 내부에서 작동하는 전처리, 최적화 정규화 기법 등의 차이가 있을 수 있습니다.
과거에 배웠던 이론을 상기시키고자 기초 이론 강의를 수강하는 것이라 실습은 진행하지 않으려했는데, 직접 mse loss와 경사하강법을 구현해보는 것이 기억에 더 남을 것 같아서 실습 및 과제 코드 리뷰를 진행했습니다.
'ML' 카테고리의 다른 글
| [ML] 시계열 데이터 - 특징, 정상성 / 비정상성, ACF, PACF, ADF (1) | 2024.07.05 |
|---|---|
| [ML] 논문구현(CSSMC) - 클래스 불균형 데이터 분류 예측을 위한 클러스터 기반 언더샘플링 기법 (0) | 2024.06.17 |
| [ML] 머신러닝 기초 (4) Linear Regression 회귀 이론 (0) | 2024.02.15 |
| [ML] 머신러닝 기초 (3) 머신러닝 기본 수학 이론 (1) | 2024.02.14 |
| [ML] 머신러닝 기초 (2) 머신러닝 기본 용어 정리 (1) | 2024.01.31 |